Estimate Accuracy Measure
Estimate accuracy is a measure of how closely the team member or group meets estimates in the tickets they log work into.
How we calculate it?
- Estimate Accuracy for task = (1 - LOGGED_HOURS_IN_TASK/ESTIMATION_OF_TASK)
- Estimate Accuracy = AVG(Estimate Accuracy for tasks)
Note: We use only done tasks with set estimation for the calculation.
How we show it?
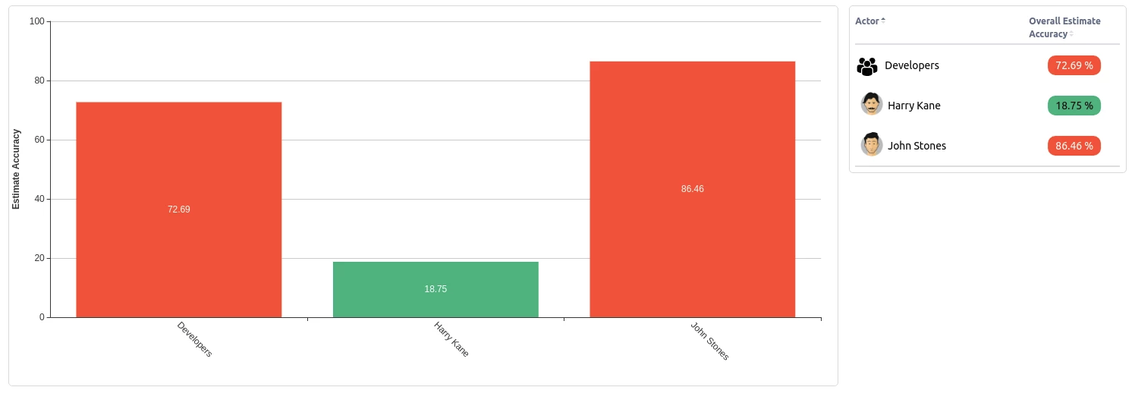
Total
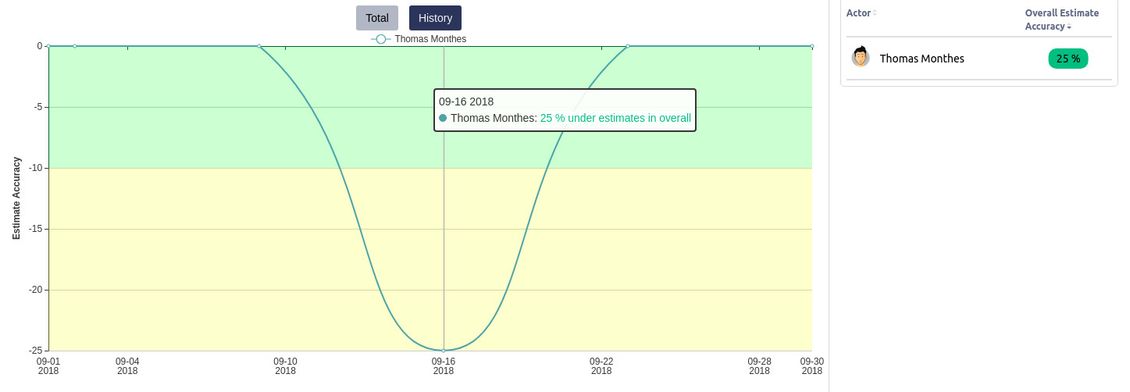
If estimate accuracy is positive, it means that on average the actor needs less time than tickets were estimated for. In table you will see these values with a green background. In the graph, you will see green bar.
If estimate accuracy is equal 0, it means that on average the actor needs exactly the time estimated in order to complete the work - he is right on the estimates. In the table you will see value on grey background with tooltip: "Exactly like estimates".
If estimate accuracy is negative, it means that on average the actor needs more time than the tickets were estimated for. In the table you will see such values on a red backgroung, the graph bar will also be red.
If there is no data for an actor to calculate "Estimate Accuracy" in table you will see "No data" message. It will not change graph. This will happen if the user didn't log any time in any matching and estimated tickets in the given time period.
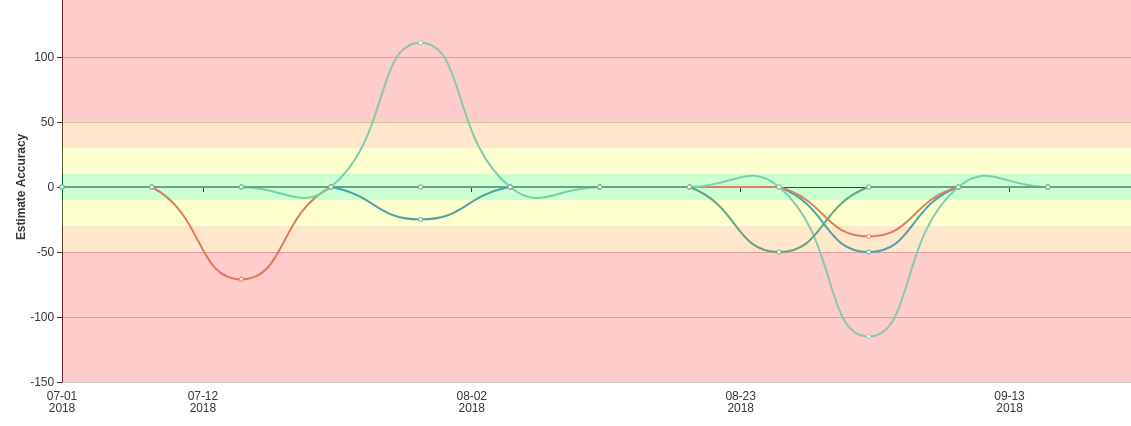
If the actor needed less time than tickets were estimated for - in the graph the value will be under X axis.
If the actor needs exactly the time estimated in order to complete the work - he is right on the estimates. In the graph the value will be 0.
If the actor needed more time than tickets were estimated for - in the graph the value will be over X axis.
Example
A user logged hours into two tickets:
Ticket | Estimate | Time logged | Estimate accuracy |
|---|---|---|---|
| EXAMPLE-1 | 1 day | 1 day 4 hours | 1 - 12h/8h = -0.5 |
| EXAMPLE-2 | 4h | 5 hours | 1 - 5h/4h = - -0.25 |
The estimate accuraccy for this user is (-0.5 -0.25)/2 = -0.375. The user is usually over the estimates by 37.5%.